Over the past few months, several open source code LLMs have been released across various sizes. Some of these offer competitive performance to OpenAI’s CodeX and ChatGPT models, especially after fine-tuning. There’s an increasing interest in deploying these LLMs to power Copilots on-premises and on individual devices. However, these models are as large as 16 Billion parameters, requiring large memory, and very slow inference time.
Today, we release a first look at LoRDCoder models on Hugging Face. These models, based on Low Rank Decomposition (LoRD), are compressed versions of open-source StarCoder LLM. You can access the v0 of these models on Hugging Face.
The design of LoRD compression was partially inspired by the effectiveness of Low-Rank Adapters (LoRA) and it offers several advantages over pruning and quantization.
Our models offer several advantages:
The weights in the LoRD model are dense. Therefore, unlike pruning, it can be parallelized better on GPUs and does not have any overhead from sparse format.
The LoRD model obviates the need for specialized kernels, in contrast to quantized models, which may even require tailoring for each target hardware. LoRD compressed models can efficiently utilize existing floating point matrix multiplication kernels available across different floating point precisions in open-source libraries like PyTorch, Jax, TinyGrad and ONNX.
The compressed neural network is fully differentiable, making the model end-to-end trainable even after compression.
All the parameters of the network are tunable and reduced parameter count provides more efficient full-parameter fine-tuning.
The LoRD model also remains LoRA tunable and adapters from the base models are compatible with the LoRD models.
The LoRD model can be further compressed via Quantization, Pruning and Distillation, to yield similar returns as its base model.
LoRD models offers these benefits with little to no performance drop.
Results on HumanEval Score
We show the results of LoRD compressed versions of the StarCoder 16B, which we dub LoRDCoder, across various parameter reduction count on the HumanEval Benchmark. The score is averaged across 5 runs and we run our evals using Code-Eval.
| Pretrained LMs | Pass at 1 | Pass at 10 |
|---|---|---|
| Replit-Code - 3B | 17.13% | 29.88% |
| Stable Code - 3B | 20.18% | 33.75% |
| CodeT5+ - 16 | 30.90% | 51.60% |
| CodeGen1 Mono - 16B | 29.28% | 49.86% |
| CodeGen2 16B | 20.28% | 36.50% |
| MPT - 30B | 25.00% | - |
| CodeGen2 16B | 20.90% | - |
| CodeGen2 16B | 20.28% | - |
| StarCoder - 16B | 31.67% | 48.29% |
| LoRDCoder V0 - 14.9B | 33.18% | 48.41% |
| LoRDCoder V0 - 14.5B | 31.69% | 45.12% |
| LoRDCoder V0 - 13.8B | 30.90% | 47.56% |
| LoRDCoder V0 - 13.2B | 31.57% | 45.36% |
| LoRDCoder V0 - 12.6B | 29.84% | 42.31 |
| LoRDCoder V0 - 12.6B | 29.22% | 40.12 |
We are able to compress the LoRDCoder models down to 13 Billion parameter dense models with no Pass@1 drop, and to 12 Billion parameters with little drop in performance. These models outperform models more than 40 times its size, including the largest LLaMa 2 model.
LoRD and Quantization
Quantization is a powerful compression method that has enabled running powerful LLMs models on mobile phones. It reduces the number of bits to represent a parameter in the model weights, thereby enabling larger models to be loaded into RAM and reducing the time for transfer between levels of memory hierarchy.
However, quantization has several shortcomings as a compression method. It requires specialized kernels, often separate for each target hardware. The resulting parameters are not differentiable and not trainable via gradient based optimization algorithms. It is LoRA tunable, but LoRA cannot be merged without additional loss. It may not reduce the FLOP count and may not offer any speedups at large batch sizes (or for encoding large LLM input prefixes/prompts), especially during fine-tuning, when compared to its floating point.
LoRD addresses all these shortcomings of quantization. And, although it does not compress to the extent that quantization does, it can be combined with quantization to deliver similar gains.
We perform compression using the SpQR quantization method over the LoRDCoder models and show its HumanEval Pass@1 score.
| Pass@1@FP16 | Pass@1@8-bit | Pass@1@4-bit | |
| LoRDCoder 14.9B | 33.18 | 33.17 | 32.01 |
| LoRDCoder 14.5B | 31.69 | 31.58 | 32.74 |
| LoRDCoder 13.8B | 30.90 | 31.10 | 30.73 |
| LoRDCoder 13.2B | 31.57 | 31.52 | 32.01 |
| LoRDCoder 12.6B | 29.84 | 29.87 | 30.22 |
| LoRDCoder 12.3B | 29.22 | 29.14 | 29.45 |
We observe minimal drop in HumanEval score after quantization to 4-bit. Surprisingly, in some cases there are minor improvements in HumanEval score as well. Such occasional phenomena of improvements from quantization have been previously observed across code LLMs.
LoRD and Unstructured Pruning
Pruning of LLMs creates sparse matrices from dense weight matrix by removing parameters (i.e. setting them to zero). However, pruned models only show improvements in inference speed and model size at very high levels of sparsity, where the LLM’s performance starts to degrade. The degradations are even higher for structured pruning at sparsity levels of as low as 50%.
LoRD technique promises to be a drop-in replacement for unstructured pruning as a method for both parameter reduction and model compression. LoRD’s dense matrices has wider than that of sparse matrices across different libraries and hardware, and dense matrix multiplications are faster on GPUs.
LoRD models have lesser model size (in GB) than pruned models at the same parameter count
Transformer inference at low batch sizes is bottlenecked by the memory bandwidth. So, smaller model size usually implies faster inference.
Sparse Matrices incur additional overhead from having to track the indices of nonzero (i.e. unpruned) elements of the weight matrix in addition to the values of the nonzero elements, where nonzero elements are the remaining model parameters. Thus, the size (in GB) of these matrices at low levels of sparsity (i.e. <60%) is much higher than that of corresponding dense matrices, even at the same number of parameters. It is only at very high levels of sparsity (at which LLMs’s performance completely degrades) that sparse matrices are smaller than dense.
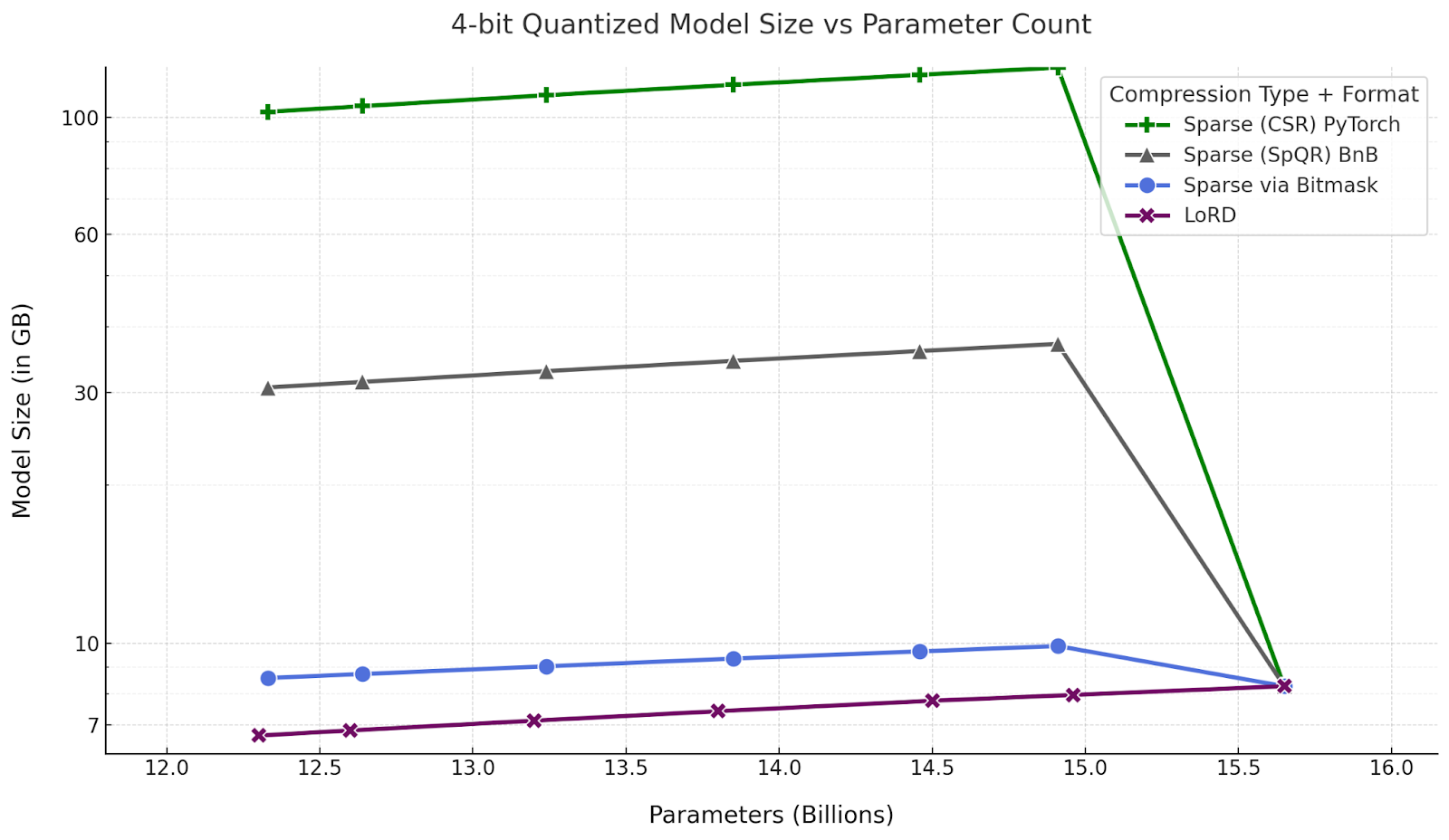
We consider 4-bit quantized model size across parameter count and compare LoRD compressed models to pruned models at three different (unstructured) sparse formats:
The dense models from LoRD compression can save upto 96 GB at similar parameter count, compared to Pytorch’s CSR sparse format. CSR is the most efficient sparse format supported by pytorch. It stores indices of nonzero elements at 64 bits. So, for a 4-bit quantization, this leads to more than 68 bits per nonzero element. PyTorch does not currently support values in CSR matrices at lower than 16-bit precision, so the actual bits per parameter will be much higher than our estimates.
LoRD compressed models can save up to 24.6 GB compared to the SoTA sparse kernels from SpQR that stores indices at 16 bits, instead of 64 bits from PyTorch. These sparse kernels were created for the floating point matrix, but assuming support for 4-bit quantization kernels, these kernels will have more than 20 bits per nonzero value of a sparse matrix. The custom sparse inference kernels of SpQR are yet to be released and merged into bitsandbytes, and our estimates were calculated based on the details in the SpQR paper.
One of the most efficient formats at low levels of sparsity is using a bitmask (i.e. 1-bit) to denote whether a value is nonzero in a matrix. This can lead to as low as 5-bit per parameter when 4-bit quantized. However, this format is impractical due to lack of low level software and hardware routines/intrinsics and is difficult to parallelize. Regardless, the LoRD model is still at least 28% more efficient than the bitmask representation method at the same parameter count.
LoRD models can also be pruned
We consider sparsifying two of the LoRDCoder models using a SoTA LLM Pruning method and compare it to the StarCoder model on the HumanEval Benchmark.
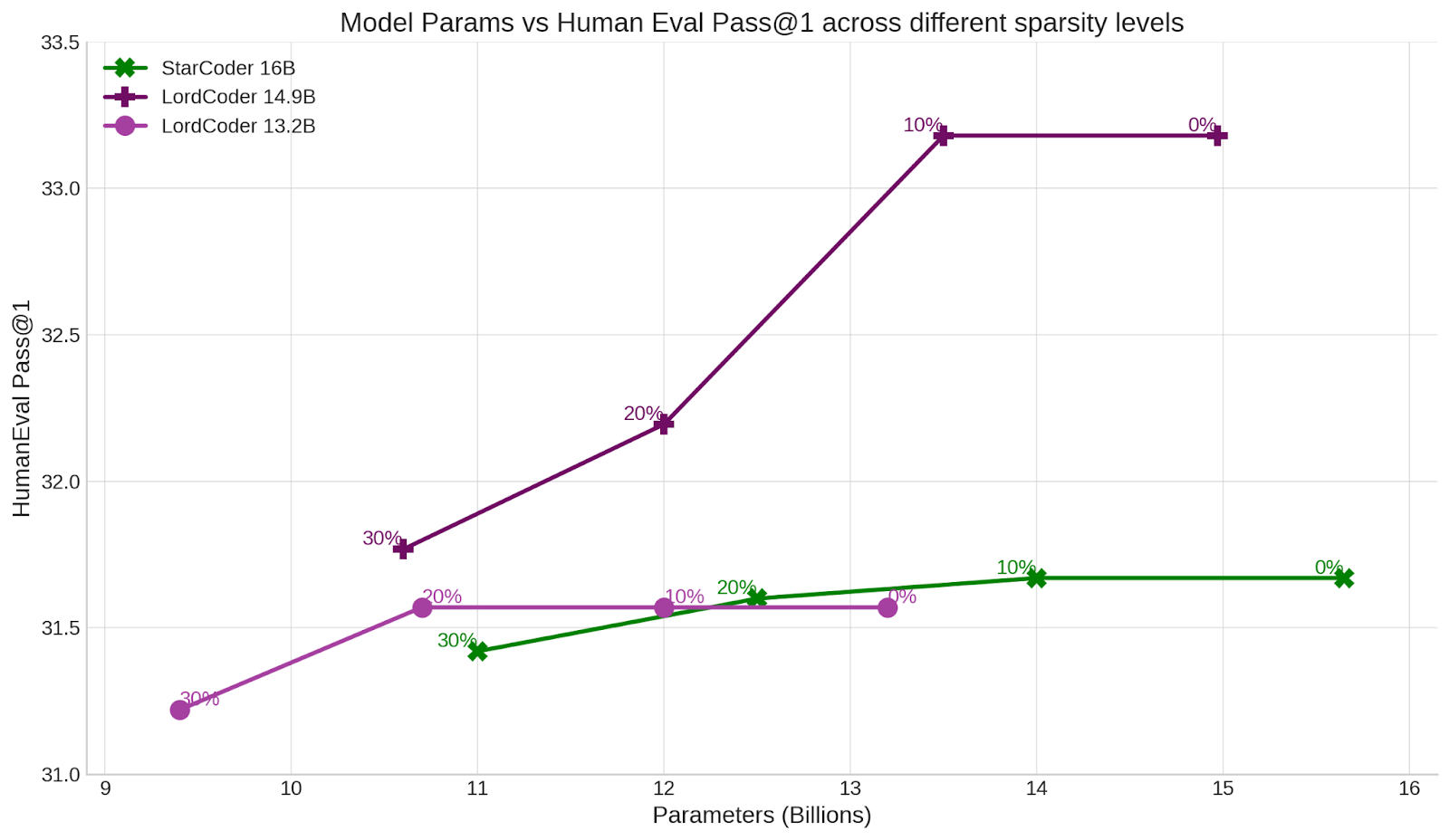We observe that LoRDCoder models can also be pruned while maintaining competitive performance.
@article{lord_llms,
title={The LoRD (Low Rank Decomposition) of Code LLMs},
author={Kaushal Ayush, Vaidhya Tejas, Rish Irina},
year={2023},
month={Aug}
}